In Natural Language Processing (NLP), understanding the order of words is just as important as understanding the words themselves. “Dog bites man” means something very different from “Man bites dog.” While traditional sequential models like Recurrent Neural Networks (RNNs) inherently process information in order, the groundbreaking Transformer architecture does not. Transformers use parallel processing, meaning all words in a sentence are processed simultaneously. This presents a critical challenge: how does a Transformer know the sequence order? The elegant solution is Positional Encoding.
The Problem: Why Order Matters and Self Attention Doesn’t Care
The core of the Transformer is its powerful self attention mechanism, which allows each word in a sequence to attend to every other word, capturing intricate relationships and context. However, by treating all words simultaneously, the model loses crucial sequence information. The word embeddings (numerical representations of words) themselves carry only semantic meaning, not positional meaning. Without a way to encode position, “dog bites man” would appear structurally identical to “man bites dog,” leading to incorrect interpretations.
What is Positional Encoding?
Positional Encoding is a technique that injects sequence information into the input embeddings of tokens before they are fed into the Transformer blocks. It is an additional vector that is added to the standard word embeddings, effectively giving each word a unique “positional fingerprint.” This allows the model to understand not just what words are present, but also where they are located relative to each other within the sequence.
How Positional Encoding Works: Types and Mechanics
There are primarily two ways positional encoding is implemented:
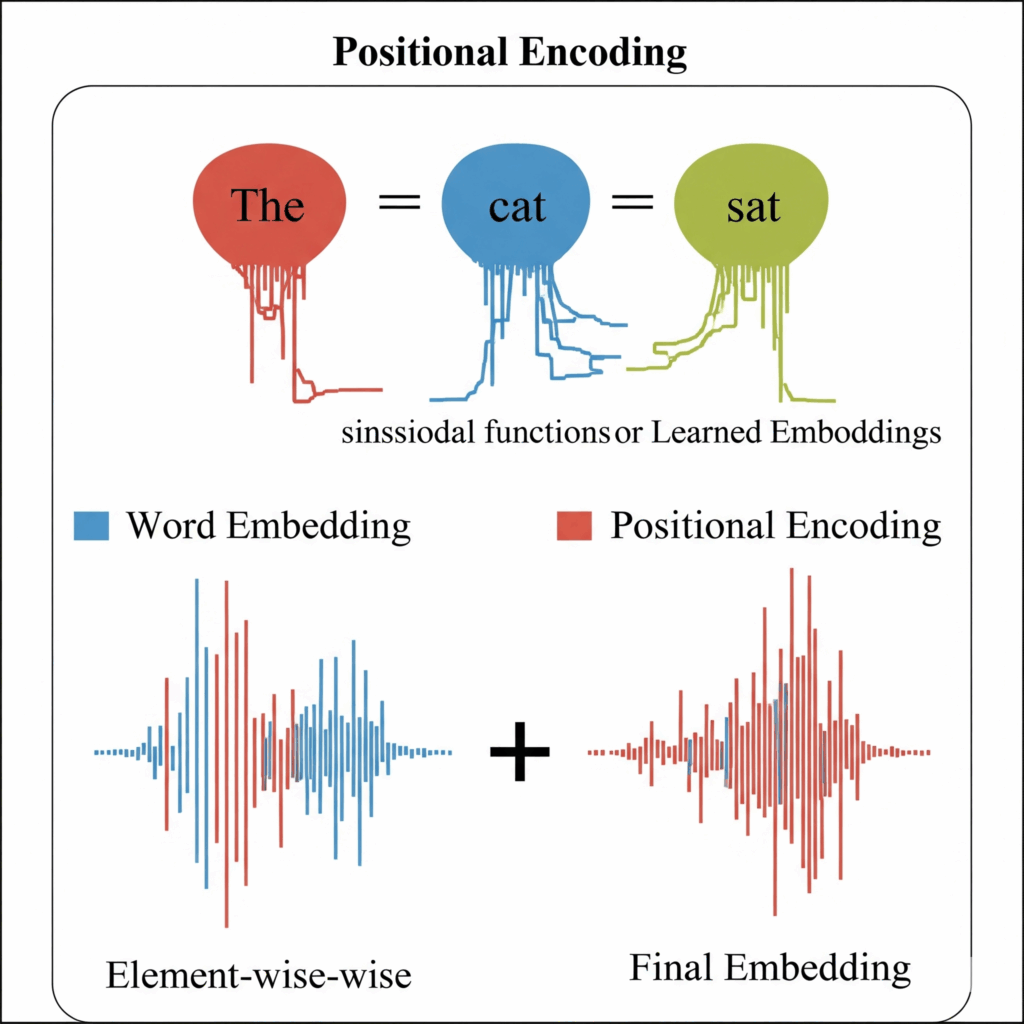
Fixed Positional Encoding (Sinusoidal Functions)
This is the method introduced in the original Transformer paper “Attention Is All You Need.” It uses deterministic mathematical sinusoidal functions (sine and cosine waves) of different frequencies to generate position vectors.
For each position pos in the sequence and each dimension i of the embedding vector (where i ranges from 0 to dmodel−1, with dmodel being the dimensionality of the embedding), the positional encoding values are calculated as follows:
PE(pos,2i)=sin(100002i/dmodelpos) PE(pos,2i+1)=cos(100002i/dmodelpos)
Here:
- pos refers to the position of the token in the sequence (e.g., 0,1,2,…).
- i refers to the dimension index within the positional embedding vector.
- dmodel is the dimensionality of the model’s embeddings.
- Advantages: It can easily generalize to sequences much longer than those seen during pretraining because the function can generate position embeddings for any length. It adds no extra parameters to learn, keeping the model simpler.
Learned Positional Encoding
As an alternative, some Transformer models simply learn the positional embeddings from scratch during the training data process. These are essentially embedding layers where each position up to a maximum sequence length has its own unique, trainable vector.
- Advantages: Potentially more flexible, as the model can learn complex positional relationships that might not be captured by fixed functions.
- Disadvantages: Cannot generalize to sequences longer than the maximum length seen during training, as there would be no learned embedding for those positions. This can impact scalability for very long texts.
Combining with Word Embeddings
Regardless of whether fixed or learned, the positional encoding vector for a given word is simply added element wise to its corresponding word embedding (or input embedding). This creates a combined embedding that carries both the semantic meaning of the word and its unique sequence information.
If Ew is the word embedding for a token and PE is its positional encoding vector, the final input embedding Einput fed into the Transformer is:
Einput=Ew+PE
This combined embedding then proceeds through the Transformer’s self attention layers.
Impact on Transformers and LLMs
Positional Encoding is absolutely critical for the success of Transformers in NLP. It is the unsung hero that enables the self attention mechanism to truly understand context based on relative position and absolute position. Without it, Transformers would treat sentences as “bags of words” losing all grammatical structure and meaning derived from word order. This mechanism is vital for language models (LLMs) to correctly interpret syntax, dependencies, and perform complex tasks, powering everything from text generation to machine translation. It directly contributes to the scalability and accuracy of modern deep learning models in NLP.
Conclusion
Positional Encoding is an ingenious and indispensable component of the Transformer architecture. It ingeniously solves the problem of encoding sequence order into parallel processed data, allowing attention mechanisms to thrive. By providing words with their “place” in the sequence, it unlocks the full potential of Transformers and has been pivotal in the rapid advancements we’ve witnessed across all areas of Natural Language Processing.



